课本提供的一些代码
(define (number x) (car x))
(define (denom x) (cdr x))
(define (print-rat x)
(newline)
(display (number x))
(display "/")
(display (denom x)))
(define (print-point p)
(newline)
(display "(")
(display (x-point p))
(display ",")
(display (y-point p))
(display ")"))
(define (add-interval x y)
(make-interval (+ (lower-bound x) (lower-bound y))
(+ (upper-bound x) (upper-bound y))))
(define (list-ref items n)
(if (= n 0)
(car items)
(list-ref (cdr items) (- n 1))))
(define (length items)
(if (null? items)
0
(+ 1 (length (cdr items)))))
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1) (append (cdr list1) list2))))
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
2.1
(define (make-rat p q)
(if (< q 0)
(cons (- p) (- q))
(cons p q)))
2.2
(define (make-point x y) (cons x y))
(define (x-point a) (car a))
(define (y-point a) (cdr a))
(define (make-segment a b) (cons a b))
(define (start-segment a) (car a))
(define (end-segment a) (cdr a))
(define (mid-point x)
(cons (/ (+ (x-point (start-segment x)) (x-point (end-segment x))) 2)
(/ (+ (y-point (start-segment x)) (y-point (end-segment x))) 2)
))
2.3
(define (make-rect1 n d) ;两个线段组成的矩形
(cons n d))
(define (lenth x)
(sqrt (+ (square (- (x-point (start-segment x)) (x-point (end-segment x))))
(square (- (y-point (start-segment x)) (y-point (end-segment x))))))) ;求矩形一边的长度
(define (a-rect x)
(car x))
(define (b-rect x)
(cdr x))
(define (make-rect2 a b c d) ;四个点组成的矩形
(cons (cons a b)
(cons c d))) ; 设 a b c d由左上角顺时针排列
(define (a-point x)
(car (car x)))
(define (b-point x)
(cdr (car x)))
(define (c-point x)
(car (cdr x)))
(define (d-point x)
(cdr (cdr x)))
(define (len1 x)
(sqrt (+ (square (- (x-point (a-point x)) (x-point (b-point x))))
(square (- (y-point (a-point x)) (y-point (b-point x)))))))
(define (len2 x)
(sqrt (+ (square (- (x-point (b-point x)) (x-point (d-point x))))
(square (- (y-point (b-point x)) (y-point (d-point x)))))))
(define (s-rect len wid)
(* len wid))
(define (c-rect len wid)
(* 2 (+ len wid)))
2.4
直接等式代换推导就可以了
(define (cdr z)
(z (lambda (p q) q)))
2.5
(define (cons x y)
(* (expt 2 x)
(expt 3 y)))
(define (car x)
(if(= 0 (remainder x 2))
(+ 1 (car (/ x 2)))
0))
(define (cdr x)
(if (= 0 remainder x 3)
(+ 1 (cdr (/ x 3)))
0))
2.6
(add-1 zero)
(lambda (f) (lambda (x) (f ((zero f) x))))
(lambda (f) (lambda (x) (f (((lambda (g) (lambda (c) c)) f) x))))
(lambda (f) (lambda (x) (f x)))
(define one
(lambda (f) (lambda (x) (f x))))
(define two
(lambda (f) (lambda (x) (f (f x)))))
加法的定义有点复杂,没想好,这里我参考了习题解
(define +
(lambda (m)
(lambda (n)
(lambda (f)
(lambda (x)
(m f (n f x)))))))
加法函数接受两个参数 m 和 n ,然后返回一个接受两个参数 f 和 x 的函数,加法函数的函数体内, n 的函数体被表达式 (n f x) 取了出来,然后又在表达式 (m f (n f x)) 中作为函数 m 的第二个函数被调用,从而将 m 和 n 函数体内的 f 调用累积起来(如果有的话),从而形成加法效果。
2.7
(define (upper-bound x)
(cdr x))
(define (lower-bound x)
(car x))
2.8
(define (sub-interval x y)
(make-interval (- (lower-bound x) (upper-bound y))
(- (upper-bound x) (lower-bound y))))
2.9
其实想要证明的就是
f(x)+f(y)=f(x+y)
f(x)+f(y)=f(x-y)
且乘除时不成立
设(upper-bound x)=(u x),(lower-bound x)=(l x)
f(x)=((u x)-(l x))/2,f(y)=((u y)-(l y))/2,
f(x)+f(y)=(((u x)+(u y))-((l x)+(l y)))/2,
f(x+y)=((u x+y)-(l x+y))/2
即(((u x)+(u y))-((l x)+(l y)))/2所以
f(x)+f(y)=f(x+y),
f(x-y)=((u x-y)-(l x-y))/2
=((u x)-(l y)-(l x)+(u y))/2,
即f(x)+f(y)=f(x-y)
乘除的情况只需要举例子就行了
a[5,15],b[15,25] wa=5,wb=5,
ab=[75,375]w(ab)=150
a/b=[0.2,1] w(a/b)=0.4
2.10
(define (div-interval x y)
(if (< (* (upper-bound y) (lower-bound y)) 0)
(display "can't div")
(mul-interval x
(make-interval (/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y))))))
2.11
做的时候发现两者下界都小于0时,要乘超过两次,上网搜才知道,翻译错了,英文是
In passing, Ben also cryptically comments: “By testing the signs of the endpoints of the intervals, it is possible to break mul-interval into nine cases, only one of which requires more than two multiplications.” Rewrite this procedure using Ben’s suggestion
(define (mul-interval x y)
(cond ((and (> (upper-bound x) 0) (> (upper-bound y) 0) (> (lower-bound x) 0) (> (lower-bound y) 0))
(make-interval (* (lower-bound x) (lower-bound y)) (* (upper-bound x) (upper-bound y))))
((and (> (upper-bound x) 0) (< (upper-bound y) 0) (> (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (* (upper-bound x) (lower-bound y)) (* (lower-bound x) (upper-bound y))))
((and (> (upper-bound x) 0) (> (upper-bound y) 0) (> (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (* (upper-bound x) (lower-bound y)) (* (upper-bound x) (upper-bound y))))
((and (> (upper-bound x) 0) (> (upper-bound y) 0) (< (lower-bound x) 0) (> (lower-bound y) 0))
(make-interval (* (lower-bound x) (upper-bound y)) (* (upper-bound x) (upper-bound y))))
((and (> (upper-bound x) 0) (> (upper-bound y) 0) (< (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (min (* (lower-bound x) (upper-bound y)) (* (upper-bound x) (lower-bound y)))
(* (upper-bound x) (upper-bound y))))
((and (> (upper-bound x) 0) (< (upper-bound y) 0) (< (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (* (upper-bound x) (lower-bound y)) (* (lower-bound x) (lower-bound y))))
((and (< (upper-bound x) 0) (> (upper-bound y) 0) (< (lower-bound x) 0) (> (lower-bound y) 0))
(make-interval (* (lower-bound x) (upper-bound y)) (* (upper-bound x) (lower-bound y))))
((and (< (upper-bound x) 0) (> (upper-bound y) 0) (< (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (* (lower-bound x) (upper-bound y)) (* (lower-bound x) (lower-bound y))))
((and (< (upper-bound x) 0) (< (upper-bound y) 0) (< (lower-bound x) 0) (< (lower-bound y) 0))
(make-interval (* (upper-bound x) (upper-bound y)) (* (lower-bound x) (lower-bound y))))
))
2.12
(define (make-center-percent c p)
(make-interval (- c (* c (/ p 100))) (+ c (* c (/ p 100)))))
(define (percent i)
(* (/ (width i) (center i)) 100))
2.13
可知px=widx/cenx=(ux-lx)/(ux+lx)
同理py=(uy-ly)/(uy+ly)
因为所有数为正,我们定义z=xy
uz=uxuy,lz=lxly
pz=(uz-lz)/(uz+lz),带入得pz=(px+py)/(pxpy+1)
2.14
(par1 (make-interval 5 10) (make-interval 20 50))
(par2 (make-interval 5 10) (make-interval 20 50))
{quasiquote {1.6666666666666667 . 20.0}}
{quasiquote {4.0 . 8.333333333333332}}
事实证明了par1和par2算出来的值完全不一样。
(define A (make-center-percent 30 20))
(define B (make-center-percent 40 30))
(div-interval A A)
(div-interval A B)
{quasiquote {0.6666666666666666 . 1.5}}
{quasiquote {0.46153846153846156 . 1.2857142857142856}}
A/A的值甚至还不为1。。。
2.15
对于par2我们可以认为影响的因子是区间的调用性,par1中r1,r2各调用了两次,par2中r1,r2只调用了一次,所以他的误差不是很大
2.16
我的判断是,涉及的非准确性变量出现次数不一样导致的运算结果出现问题,至于设计一个算术包,确实想不太出来。接下来将参考网络上的答案
可以看到,由于不确定的值a用了多次后,结果的误差更大了。这和习题2.15是所说的是相符的。
对于问题2,到底能不能设计出一种能够避免上面的区间运算包,我觉得只要能够去掉不确定性值的不确定性就可以了。 我们可以实现一个identity函数,在使用某个区间前先判断其是否与之前使用过的区间相等,如果相等,直接取上次的结果就可以了。
在下面给出的参考链接3中,发现我这个想法是不可能的,wiki上称之为Dependency_problem:
The so-called dependency problem is a major obstacle to the application of interval arithmetic. Although interval methods can determine the range of elementary arithmetic operations and functions very accurately, this is not always true with more complicated functions. If an interval occurs several times in a calculation using parameters, and each occurrence is taken independently then this can lead to an unwanted expansion of the resulting intervals.
…
In general, it can be shown that the exact range of values can be achieved, if each variable appears only once. However, not every function can be rewritten this way.区间运算问题也很有名,下面给出几个链接,后面有机会再深入了解:https://en.wikipedia.org/wiki/Interval_arithmetic
http://www.cs.utep.edu/interval-comp/main.html
2.17
(define (last-pair items)
(if (null? (cdr items))
(car items)
(last-pair (cdr items))))
2.18
(define (reverse items)
(define (reverse-iter items n)
(if(= n -1)
'()
(cons (list-ref items n) (reverse-iter items (- n 1)))))
(reverse-iter items (- (length items) 1)))
(reverse (list 1 2 3 4))
2.19
(define (except-first-denomination coin-values)
(cdr coin-values))
(define (first-denomination coin-values)
(car coin-values))
(define (no-more? coin-values)
(null? coin-values))
不会,更改顺序其实只是将拿取一种货币的事件进行了对调而已,从整体上而言无论怎么调换都会统计得到,所以不影响输出结果
2.20
(define (same-parity first . elses)
(filter (if (even? first)
even?
odd?)
(cons first elses)))
2.21
(define (square-list items)
(if (null? items)
nil
(cons (square (car items)) (cdr items))))
(define (square-list items)
(map (lambda (x) (* x x)) items))
2.22
因为它每次把最里面的元素更新时放在集合的car部分所以失败了
第二种只是调换了位置,导致在car处使用的cons最多,得到的不是我们想要的list结构,反而是((number2),number1)这样的结构
2.23
加个not来避免末尾时的操作
(define (for-each proc items)
(if (not (null? items))
(begin
(proc (car items))
(for-each proc (cdr items)))))
2.24
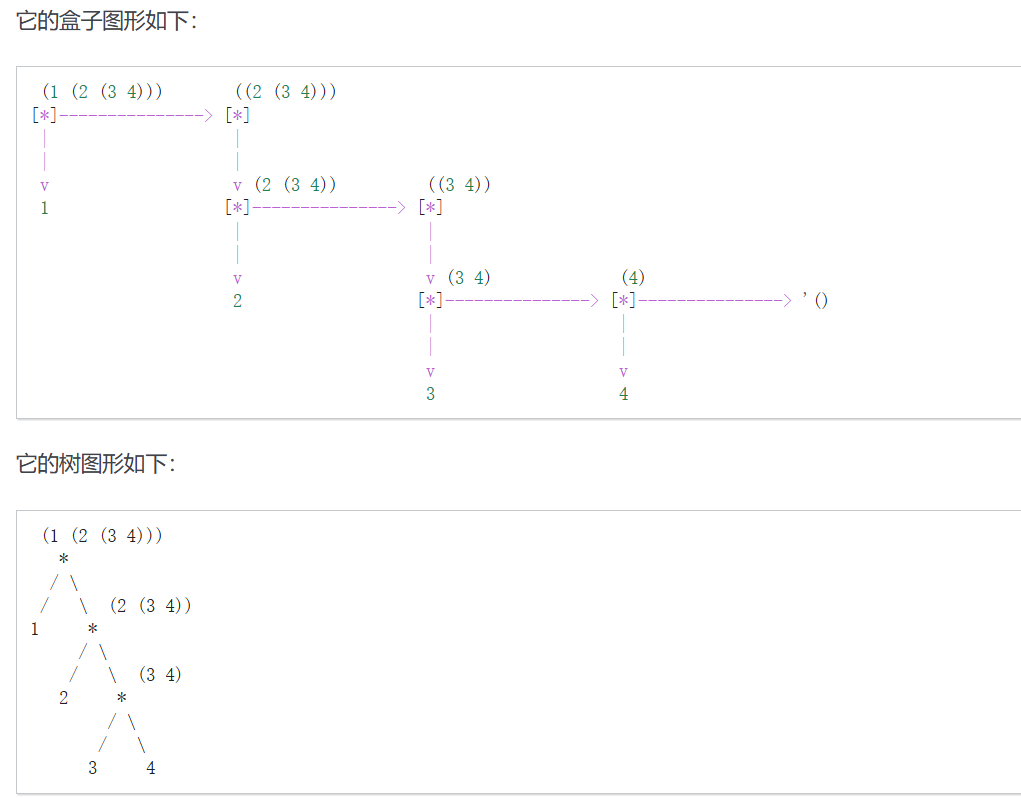
(list 1 (list 2 (list 3 4)))
(1 (2 (3 4)))
盒子图形和树图形引用于习题解
2.25
(define a (list 1 3 (list 5 7) 9))
(car(cdaddr a))
(define b (list (list 7)))
(caar b)
(define c (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 (list 7))))))))
(car(cadadr(cadadr (cadadr c))))
2.26
(define x (list 1 2 3))
(define y (list 4 5 6))
(append x y)
(cons x y)
(list x y)
(1 2 3 4 5 6)
((1 2 3) 4 5 6)
((1 2 3) (4 5 6))
2.27
(define (deep-reverse items)
(define (reverse-iter items n)
(if(= n -1)
'()
(if (pair? (list-ref items n))
(cons (deep-reverse(list-ref items n)) (reverse-iter items (- n 1)))
(cons (list-ref items n) (reverse-iter items (- n 1))))))
(reverse-iter items (- (length items) 1)))
2.28
(define (fringe x)
(if (null? x)
'()
(if (pair? x)
(append (fringe(car x)) (fringe (cadr x)))
(list x))))
2.29
c比较难做,核心还是利用pair?来递归检测
(define (left-branch x)
(car x))
(define (right-branch x)
(cadr x))
(define (branch-length x)
(car x))
(define (branch-structure x)
(cadr x))
(define (total-weight x)
(define (branch-weight y)
(if (pair? (branch-structure y))
(total-weight (branch-structure y))
(branch-structure y)))
(+ (branch-weight (left-branch x)) (branch-weight (right-branch x))))
(c)参考了解题集
(define (hangs-another-mobile? branch)
(pair? (branch-structure branch)))
(define (branch-weight y)
(if (pair? (branch-structure y))
(total-weight (branch-structure y))
(branch-structure y)))
(define (branch-torque branch)
(* (branch-length branch)
(branch-weight branch)))
(define (mobile-balance? mobile)
(let ((left (left-branch mobile))
(right (right-branch mobile)))
(and
(same-torque? left right)
(branch-balance? left)
(branch-balance? right))))
(define (same-torque? left right)
(= (branch-torque left)
(branch-torque right)))
(define (branch-balance? branch)
(if (hangs-another-mobile? branch)
(mobile-balance? (branch-structure branch))
#t))
(define (left-branch x)
(car x))
(define (right-branch x)
(cdr x))
(define (branch-length x)
(car x))
(define (branch-structure x)
(cdr x))
2.30
(define (square-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (square tree))
(else (cons (square-tree (car tree))
(square-tree (cdr tree))))))
(define (square-tree tree)
(map (lambda (sub-tree)
(if(pair? sub-tree)
(square-tree sub-tree)
(square sub-tree))) tree))
2.31
(define (tree-map f tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(tree-map f sub-tree)
(f sub-tree))) tree))
2.32
(define (subsets s)
(if (null? s)
(list nil)
(let ((rest (subsets (cdr s))))
(append rest (map (lambda (x) (cons (car s) x)) rest)))))
原理是拿或者不拿,都必须要将数据粘合起来,就需要用到cons。
2.33
(define (map p sequence)
(accumulate (lambda (x y) (cons (p x) y)) nil sequence))
(define (append seq1 seq2)
(accumulate cons seq2 seq1))
(define (length sequence)
(accumulate (lambda (x y) (+ y 1)) 0 sequence))
2.34
(define (horner-eval x coefficient-sequence)
(accumulate (lambda (this-coeff higher-terms) (+ this-coeff (* x higher-terms)))
0
coefficient-sequence))
注意是次幂最低的先提出去
2.35
(define (count-leave t)
(accumulate + 0 (map (lambda (x)
(if (pair? x)
(count-leave x)
1))
t)))
计算叶节点,积累时合并。
2.36
这题没什么思路,主要还是我不知道能用之前的函数,如果知道要用之前的函数,马上就做完了。map返回的还是一个list,所以能符合要求。
(define (accumulate-n op init seqs)
(if (null? (car seqs))
nil
(cons (accumulate op init (map car seqs))
(accumulate-n op init (map cdr seqs)))))
2.37
(define (matrix-*-vector m v)
(map (lambda (x) (dot-product x v) m)))
(define (transpose mat)
(accumulate-n cons '() mat))
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map (lambda (x) (matrix-*-vector cols x)) m)))
2.38
(define (fold-left op initial sequence)
(define (iter result rest)
(if (null? rest)
result
(iter (op result (car rest))
(cdr rest))))
(iter initial sequence))
(define (fold-right op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(fold-right op initial (cdr sequence)))))
(fold-right / 1 (list 1 2 3))
(fold-left / 1 (list 1 2 3))
(fold-right list nil (list 1 2 3))
(fold-left list nil (list 1 2 3))
#e1.5
#e0.16
(1 (2 (3 ())))
(((() 1) 2) 3)
我觉得op就是要满足对称性,像\div就不满足A/B=B/A然鹅习题解说是满足结合律。。
## 2.39
(define (reverse sequence)
(fold-right (lambda (x y) (append y (list x))) nil sequence))
(define (reverse sequence)
(fold-left (lambda (x y) (cons y x)) nil sequence))
主要在于fold-right怎么去掉多余的括号,采用append和将x强制转换类型是一个比较好的选择。
2.40
(define (enumerate-interval x n)
(if (< n x)
'()
(cons x (enumerate-interval (+ x 1) n))))
(define (flatmap proc seq)
(accumulate append nil (map proc seq)))
(define (unique-pairs n)
(flatmap (lambda (i)
(map (lambda (j) (list i j)) (enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))
(define (prime-sum? pair)
(prime? (+ (car pair) (cadr pair))))
(define (make-pair-sum pair)
(list (car pair) (cadr pair) (+ (car pair) (cadr pair))))
(define (prime-sum-pairs n)
(map make-pair-sum
(filter prime-sum? (unique-pairs n))))
2.41
(define (unique-triples n)
(flatmap (lambda (i)
(map (lambda (j)
(cons i j))
(unique-pairs (- i 1))))
(enumerate-interval 1 n)))
(define (sum-bool? s seq)
(= s (+ (car seq) (cadr seq) (caddr seq))))
(define (tri-sum s)
(filter (lambda (x)
(sumbool? s x))
(unique-triples s)))
2.42
观察代码会发现最里层的adjoin-position和我们之前的unique-triples类型差不多就是多了个k但是这个k我怎么想都觉得多余,看了解题集还真是多余的。。。。。接下来的安全检查就有点麻烦了。
(define empty-board '())
(define (adjoin-position new-row k rest-of-queens)
(cons rest-of-queens new-row)
)
(define (safe? k position)
(define (iter-exam x rest i);每次都是取出排头进行检查
(cond ((null? rest) #t)
((or (= x (car rest)) ;用来模拟列和对角线的检查
(= x (+ i (car rest)))
(= x (- (car rest) i))) #f)
(else (iter-exam x (cdr rest) (+ i 1)))))
(iter-exam (car position)
(cdr position)
1))
2.43
调换了顺序结果导致每次调用(queen-cols k)的(enumerate-interval 1 board-size)的一个k,都要获得一个 (queen-cols (- k 1)),而原来的是一个(queen-cols k)调用一次 (enumerate-interval 1 board-size)返回一个queen-cols (- k 1)),所以新改的时间量相当于 T * board-size。
2.44
(define (up-spilt painter n)
(if (= n 0)
painter
(let ((smaller (right-spilt painter (- n 1))))
(below painter (beside smaller smaller)))))
2.45
这里有自身的调用,使用lambda会非常棘手
(define (spilt comb-a comb-b)
(define (p-n painter n)
(if (= n 0)
painter
(let ((smaller (p-n painter (- n 1))))
(comb-a painter (comb-b smaller smaller)))))
p-n)
2.46
(define (make-vect x y)
(cons x y))
(define (xcor-vect a)
(car a))
(define (ycor-vect a)
(cdr a))
(define (add-vect a b)
(cons (+ (xcor-vect a) (xcor-vect b)) (+ (ycor-vect a) (ycor-vect b))))
(define (sub-vect a b)
(cons (- (xcor-vect a) (xcor-vect b)) (- (ycor-vect a) (ycor-vect b))))
(define (scale-vect s a)
(cons (* s (xcor-vect a)) (* s (ycor-vect a))))
2.47
(define (make-frame origin edge1 edge2)
(list origin edg1 edg2))
(define (origin-frame x)
(car x))
(define (edge1-frame x)
(cadr x))
(define (edge2-frame x)
(caddr x))
(define (make-frame origin edge1 edge2)
(cons origin (cons edge1 edge2)))
(define (origin-frame x)
(car x))
(define (edge1-frame x)
(car (cdr x)))
(define (edge2-frame x)
(cdr (cdr x)))
2.48
(define (make-segment a b)
(cons a b))
(define (start-segment x)
(car x))
(define (end-segment x)
(cdr x))
2.49
参考了https://blog.zwlin.io/post/sicp-2/ 的解答
(define left-bottom (make-vect 0 0))
(define left-top (make-vect 0 1))
(define right-bottom (make-vect 1 0))
(define right-top (make-vect 1 1))
(define mid-bottom (make-vect 0 0))
(define mid-top (make-vect 0 1))
(define mid-left (make-vect 1 0))
(define mid-right (make-vect 1 1))
;Q(a)
(paint (segments->painter (list (make-segment left-bottom left-top)
(make-segment left-top right-top)
(make-segment right-top right-bottom)
(make-segment right-bottom left-bottom))))
(newline)
;Q(b)
(paint (segments->painter (list (make-segment left-bottom right-top)
(make-segment left-top right-bottom))))
(newline)
;Q(c)
(paint (segments->painter (list (make-segment mid-left mid-top)
(make-segment mid-top mid-right)
(make-segment mid-right mid-bottom)
(make-segment mid-bottom mid-left))))
(segments->painter (list
(make-segment (make-vect 0.4 1.0) ; 头部左上
(make-vect 0.35 0.85))
(make-segment (make-vect 0.35 0.85) ; 头部左下
(make-vect 0.4 0.64))
(make-segment (make-vect 0.4 0.65) ; 左肩
(make-vect 0.25 0.65))
(make-segment (make-vect 0.25 0.65) ; 左手臂上部
(make-vect 0.15 0.6))
(make-segment (make-vect 0.15 0.6) ; 左手上部
(make-vect 0.0 0.85))
(make-segment (make-vect 0.0 0.65) ; 左手下部
(make-vect 0.15 0.35))
(make-segment (make-vect 0.15 0.35) ; 左手臂下部
(make-vect 0.25 0.6))
(make-segment (make-vect 0.25 0.6) ; 左边身体
(make-vect 0.35 0.5))
(make-segment (make-vect 0.35 0.5) ; 左腿外侧
(make-vect 0.25 0.0))
(make-segment (make-vect 0.6 1.0) ; 头部右上
(make-vect 0.65 0.85))
(make-segment (make-vect 0.65 0.85) ; 头部右下
(make-vect 0.6 0.65))
(make-segment (make-vect 0.6 0.65) ; 右肩
(make-vect 0.75 0.65))
(make-segment (make-vect 0.75 0.65) ; 右手上部
(make-vect 1.0 0.3))
(make-segment (make-vect 1.0 0.15) ; 右手下部
(make-vect 0.6 0.5))
(make-segment (make-vect 0.6 0.5) ; 右腿外侧
(make-vect 0.75 0.0))
(make-segment (make-vect 0.4 0.0) ; 左腿内侧
(make-vect 0.5 0.3))
(make-segment (make-vect 0.6 0.0) ; 右腿内侧
(make-vect 0.5 0.3))))
2.50
(define (flip-horiz painter)
(transform-painter painter
(make-vect 1.0 0)
(make-vect 0 0)
(make-vect 1.0 1.0)))
(define (rotate180 painter)
(transform-painter painter
(make-vect 1.0 1.0)
(make-vect 0 1.0)
(make-vect 1.0 0)))
(define (rotate270 painter)
(transform-painter painter
(make-vect 0 1.0)
(make-vect 0 0)
(make-vect 1.0 1.0)))
2.51
参考了解题集
(define (below painter1 painter2)
(let((spilt-point (make-vect 0.5 0)))
(let ((paint-down
(transform-painter painter1
(make-vect 0 0)
(make-vect 1.0 0)
(spilt-point)))
(paint-up
(transform-painter painter2
spilt-point
(make-vect 1.0 0.5)
(make-vect 0 1.0)))
(lambda (frame)
(paint-down frame)
(paint-up frame))))))
(define (below painter1 painter2)
(lambda (frame)
((flip-horiz
(rotate90
(beside
(rotate270
(flip-horiz painter1))
(rotate270
(flip-horiz painter2)))))
frame)))
2.52
(segments->painter (list (make-segment (make-vect 0 0)
(make-vect 1 1))))
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1)))
(corner (corner-split painter (- n 1))))
(beside (below painter up)
(below right corner)))))
(define (square-limit painter n)
(let ((combine4 (square-of-four identity flip-horiz)
flip-vect rotate180))
(combine4 (corner-split painter n))))
2.53
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))
(list 'a 'b 'c)
(list (list 'george))
(cdr '((x1 x2) (y1 y2)))
(cadr '((x1 x2) (y1 y2)))
(pair? (car '(a short list)))
(memq 'red '((red shoes) (bule socks)))
(memq 'red '(red shoes bule socks))
(a b c)
((george))
((y1 y2))
(y1 y2)
#f
#f
(red shoes bule socks)
2.54
(define (equal? a b)
(cond ((and (null? a) (null? b)) #t)
((not (eq? (car a) (car b))) #f)
(else (equal? (cdr a) (cdr b)))))
2.55
实际上是求值
(car '(quote abracadabra))
2.56
(define (exponentiation? exp)
(eq? '** (car exp)))
(define (base exp)
(cadr exp))
(define (expoent exp)
(caddr exp))
(define (make-exponentiation base expoent)
(cond ((= expoent 0) 1)
((= expoent 1) base)
(else (list '** base expoent))))
((exponentiation? exp);直接复制进去就行了
(make-product (expoent exp)
(make-product (make-exponentiation (base exp) (- (expoent exp) 1))
(deriv (base exp) var))))
2.57
做的时候忘记了.可以传入多个参数。。
以下参考习题解
加法:
(define (single-operand? x) (= 1 (length x)))
(define (make-sum a1 . a2)
(if (single-operand? a2)
(let ((a2 (car a2)))
(cond ((=number? a1 0)
a2)
((=number? a2 0)
a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else
(list '+ a1 a2))))
(cons '+ (cons a1 a2))))
(define (sum? x)
(and (pair? x)
(eq? (car x) '+)))
(define (addend s)
(cadr s))
(define (augend s)
(let ((tail-operand (cddr s)))
(if (single-operand? tail-operand)
(car tail-operand)
(apply make-sum tail-operand))))
乘法:
(define (single-operand? x) (= 1 (length x)))
(define (make-product m1 . m2)
(if (single-operand? m2)
(let ((m2 (car m2)))
(cond ((or (=number? m1 0) (=number? m2 0))
0)
((=number? m1 1)
m2)
((=number? m2 1)
m1)
((and (number? m1) (number? m2))
(* m1 m2))
(else
(list '* m1 m2))))
(cons '* (cons m1 m2))))
(define (product? x)
(and (pair? x)
(eq? (car x) '*)))
(define (multiplier p)
(cadr p))
(define (multiplicand p)
(let ((tail-operand (cddr p)))
(if (single-operand? tail-operand)
(car tail-operand)
(apply make-product tail-operand))))
这里用到了新的函数apply:
apply函数是一个高阶函数,它接受两个参数:一个函数和一个参数列表。它将函数应用于参数列表中的所有元素,并返回一个新的列表,其中包含每个参数的函数应用结果
2.58
(define (make-sum a1 a2)
(cond ((=number? a1 0)
a2)
((=number? a2 0)
a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else (list a1 '+ a2))))
(define (sum? x)
(and (pair? x)
(eq? (cadr x) '+)))
(define (addend x)
(car x))
(define (augend x)
(caddr s))
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0))
0)
((=number? m1 1)
m2)
((=number? m2 1)
m1)
((and (number? m1) (number? m2))
(* m1 m2))
(else
(list m1 '* m2))))
(define (product? x)
(and (pair? x)
(eq? (cadr x) '*)))
(define (multiplier p)
(car p))
(define (multiplicand p)
(caddr p))
我觉得不太行,因为程序检测的时候需要对不同的+查看优先度,而优先度在构造选择这些函数是不能表现出来的,必须要修改deriv函数来优先寻找*这样的类型。
2.59
(define (union-set set1 set2)
(cond ((null? set1) set2)
((element-of-set? (car set1) set2)
(union-set (cdr set1) set2))
(else (cons (car set1)
(union-set (cdr set1) set2)))))
2.60
(define (element-of-set? x set)
(cond ((null? set)
#f)
((equal? x (car set))
#t)
(else
(element-of-set? x (cdr set)))))
(define (adjoin-set x set)
(cons x set))
(define (union-set set1 set2)
(cond ((null? set1) set2)
((element-of-set? (car set1) set2)
(union-set (cdr set1) set2))
(else (cons (car set1)
(union-set (cdr set1) set2)))));也可以用于重复集合,但如果想要全部保留,可以直接用append函数表示。
(define (intersection-set set1 set2)
(define (iter s1 s3)
(if (or (null? s1) (null? set2))
s3
(if (and (element-of-set? (car s1) set2)
(not (element-of-set? (car s1) s3)))
(iter (cdr s1)
(cons (car s1) s3))
(iter (cdr s1) s3))))
(iter set1 '()))
最后发现adjoin时间复杂度下降到了1,其他都没有改变,所以涉及到高频率的数据插入时需要使用有重复版。
2.61
(define (adjoin-set x set)
(cond ((null? set) (cons x set))
((and (< (car set) x) (> (cadr set) x)) (cons (car set) (cons x (cdr set))))
((= x (car set)) set)
(else (cons (car set) (adjoin-set x (cdr set))))))
类似element-of-set?的查找,时间复杂度为n/2。
2.62
(define (union-set set1 set2)
(cond ((and (null? set1) (null? set2))
'())
((null? set1) set2)
((null? set2) set1)
((= (car set1) (car set2))
(cons (car set1) (union-set (cdr set1) (cdr set2))))
((< (car set1) (car set2))
(cons (car set1) (union-set (cdr set1) set2)))
((> (car set1) (car set2))
(cons (car set2) (union-set set1 (cdr set2))))))
2.63
两种办法出来的表都是一样的,且都是排序好的
list1需要额外调用append,而它时间复杂度为n,而对于每次调用list1都需要调用一次,转换成表需调用n次list1,所以总体时间复杂度为n^2,而list2只调用cons时间复杂度为n。
2.64
参考了解题集
(a)
(b):list->tree 都要执行一次 make-tree,而make-tree的时间复杂度为1,所以总体的时间复杂度为n
2.65
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if(null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list (right-branch tree)
(result-list))))))
(copy-to-list tree '()))
(define (list-tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result (partial-tree (cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts (cdr right-result)))
(cons (make-tree this-entry left-tree right-tree)
remaining-elts))))))))
实际上用三个时间复杂度为n的组合在一起就好了
(define (intersection-tree tree1 tree2)
(list->tree
(intersection-set (tree->list-2 tree1)
(tree->list-2 tree2))))
(define (union-tree tree1 tree2)
(list->tree
(union-set (tree->list-2 tree1)
(tree->list-2 tree2))))
2.66
抽象来看实际上还是element-of-set?的修改,将节点由先前的数换为了一个类集合的东西,实际上这个设计思想就是哈希表。
(define (lookup-tree given-key tree)
(cond ((null? tree) #f)
((= given-key (key (entry tree))) true)
((< given-key (key (entry tree))) (lookup-tree given-key (left-branch tree)))
((> given-key (key (entry tree))) (lookup-tree given-key (right-branch tree)))))
2.67
(define (make-leaf symbol weight)
(list 'leaf symbol weight))
(define (leaf? object)
(eq? 'leaf (car object)))
(define (symbol-leaf x)
(cadr x))
(define (weight-leaf x)
(caddr x))
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
(define (left-branch tree)
(car tree))
(define (right-branch tree)
(cadr tree))
(define (symbols tree)
(if(leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if(leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit -- CHOOSE-BRANCH" bit))))
(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set))))))
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair)
(cadr pair))
(make-leaf-set (cdr pairs))))))
(define sample-tree
(make-code-tree (make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(decode sample-message sample-tree)
(A D A B B C A)
2.68
本来写的是一个递归的函数,但是没法确定怎么令找不到的进程停止,看了解题集才知道需要引入一个辅助函数,这也体现了对tree的symbol元素没有充分利用。
解题集的find函数没学过,自己重写了一遍辅助函数。
(define (encode-symbol x tree)
(cond ((leaf? tree)'())
((symbol-in-tree? x (left-branch tree)) (cons 0 (encode-symbol x (left-branch tree))))
((symbol-in-tree? x (right-branch tree)) (cons 1 (encode-symbol x (right-branch tree))))
(else (error "Symbol is not in tree" x))))
(define (symbol-in-tree? x tree)
(define (iter x s)
(cond ((null? s) #f)
((eq? (car s) x) #t)
(else (iter x (cdr s)))))
(iter x (symbols tree)))
2.69
(define (generate-huffman-tree pairs)
(successive-merge (make-leaf-set pairs)))
(define (successive-merge ordered-set)
(define (sucessive-merge tree)
(cond ((= 0 (length tree)) '())
((= 1 (length tree)) (car tree))
(else (sucessive-merge (adjoin-set
(make-code-tree (car tree)
(cadr tree))
(cddr tree))))))
使用adjoin-set来进行合并之后的再排序就行了
2.70
(define tree (generate-huffman-tree '((A 1) (NA 16) (BOOM 1) (SHA 3) (GET 2) (YIP 9) (JOB 2) (WAH 1))))
(1 1 0 0 1 1 1 1 0 1 1 1 1 1)
(1 1 1 0 0 0 0 0 0 0 0 0)
(1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0)
(1 1 1 0 1 1 0 1 1)
位数量:msg1=14,msg2=12,msg3=23,msg4=9
所需的二进制数量为14*2+12*2+23+9=84
其中 msg1和msg2出现了两次,所以数量要乘以2。
如果采用定长编码,那么8个字符最少每个要占用3个二进制位,而未编码的原文总长度为3*2+9*2+10+2=36,那么使用定长编码所需的二进制位为36*3=108。
使用huffman编码比使用定长编码节省了24个二进制位。
2.71
*
/\
* 16
/\
* 8
/ \
* 4
/\
1 2
*
/\
* 512
/\
* 256
/\
* 128
/\
* 64
/\
* 32
/\
* 16
/\
* 8
/ \
* 4
/\
1 2
最频繁是1个二进制位,最不频繁是n-1个二进制位
2.72
假设有n个字符,最频繁时每次都要调用一次,所以时间复杂度为n
而最不频繁时每次要调用n-1次,所以时间复杂度是n^2
2.73
(a)这是因为在scheme中,数字被直接表示为scheme的数值类型,而变量被直接表示为scheme的符号类型,所以没有必要加入到包中
(b)
(define (addend x)
(car x))
(define (augend x)
(cadr x))
(define (make-sum x y)
(cond ((=number? x 0)
y)
((=number? y 0)
x)
((and (number? x) (number? y))
(+ x y))
(else (attach-tag '+ x y))))
(put 'addend '+ addend)
(put 'augend '+ augend)
(put 'make-sum '+ make-sum)
(put 'deriv '+ (lambda (exp var)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var))))
(define (make-sum x y)
((get 'make-sum '+) x y))
(define (addend sum)
((get 'addend '+) (contents sum)))
(define (augend sum)
((get 'augend '+) (contents sum)))
(define (multiplier x)
(car x))
(define (multiplicand x)
(cadr x))
(define (make-product x y)
(cond ((=number? x 1)
y)
((=number? y 1)
x)
((or (=number? x 0) (=number? y 0))
0)
((and (number? x) (number? y))
(* x y))
(else
(attach-tag '* x y))))
(put 'multiplier '* multiplier)
(put 'multiplicand '* multiplicand)
(put 'make-product '* make-product)
(put 'deriv '* (lambda (exp var)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp)))))
(define (make-product x y)
((get 'make-product '*) x y))
(define (multiplier product)
((get 'multiplier '*) (contents product)))
(define (augend product)
((get 'multiplicand '*) (contents product)))
(c)
(define (base x)
(car x))
(define (exponent x)
(cadr x))
(define (make-power x y)
(cond ((or (=number? x 1) (=number? y 0))
1)
((or (=number? y 1) (=number? x 0))
x)
(else (attach-tag '** x y))))
(put 'base '** base)
(put 'exponent '** exponent)
(put 'make-power '** make-power)
(put 'deriv '** (lambda (exp var)
(make-product
(exponent exp)
(make-product
(make-power (base exp) (- (exponent 1)))
(deriv (base exp) var)))))
(define (make-power x y)
((get 'make-power '**) x y))
(define (base power)
((get 'base '**) (contents power)))
(define (exponent power)
((get 'exponent '**) (contents power)))
(d)将成员名称和运算符调换位置
如
(put 'make-sum '+ make-sum)
改为
(put '+ 'make-sum make-sum)
2.74
引用于解题集
题目给出的条件和帮助都不够明确,如果按照书本给出的知识的话,是没办法完成这道题的,因为涉及到的知识比如 IO 操作都没有讲,因此忽略这道题。
解题的思路和使用包的思路一样,将每个公司作为一个 tag ,将薪水和职位等信息域作为第二个 tag ,然后使用数据分派方式,就可以实现不同公司之间的通用操作了。
2.75
(define (make-form-mag-ang x y)
(define (dispatch op)
(cond ((eq? op 'real-part)
(* x (cos y)))
((eq? op 'imag-part)
(* x (sin y)))
((eq? op 'magnitute) x)
((eq? op 'ang) y)
(else
(error "Unknown op -- MAKE-FROM-MAG-ANG" op))))
(dispatch))
2.76
引用于解题集
显式分派: 这种策略在增加新操作时需要使用者避免命名冲突,而且每当增加新类型时,所有通用操作都需要做相应的改动,这种策略不具有可加性,因此无论是增加新操作还是增加新类型,这种策略都不适合。
数据导向:数据导向可以很方便地通过包机制增加新类型和新的通用操作,因此无论是增加新类型还是增加新操作,这种策略都很适合。
消息传递:消息传递将数据对象和数据对象所需的操作整合在一起,因此它可以很方便地增加新类型,但是这种策略不适合增加新操作,因为每次为某个数据对象增加新操作之后,这个数据对象已有的实例全部都要重新实例化才能使用新操作。
2.77
程序执行下去会出现这个现象
(get 'magnitude '(complex))
可以知道这是未定义行为,所以如Alyssa所说我们要定义选择函数才能解决。
(magnitude z)
(apply-generic 'magnitude z)
(map type-tag (list z))
(get 'magnitude '(complex))
(apply magnitude (map contents (list z)))
(magnitude '(rectangular 3 . 4))
(apply-generic 'magnitude '(rectangular 3 . 4))
(map type-tag (list '(rectangular 3 . 4)))
(get 'magnitude '(rectangular))
(apply magnitude (map contents (list '(rectangular 3 . 4))))
(magnitude '(3 . 4))
(sqrt (+ (square (real-part '(3 . 4)))
(square (imag-part '(3 . 4)))))
apply-generic 调用了两次,第一次调用拆去了complex的符号,并调用(install-rectangular-package)包中的magnitude 函数;第二次调用它拆去了rectangular的符号
2.78
(define (attach-tag type-tag contents)
(if (number? contents)
contents
(cons type-tag contents)))
(define (type-tag datum)
(cond ((number? datum)
'scheme-number)
((pair? datum)
(car datum))
(else
(error "Bad tagged datum -- TYPE-TAG" datum))))
(define (contents datum)
(cond ((number? datum)
datum)
((pair? datum)
(cdr datum))
(else
(error "Bad tagged datum -- CONTENT" datum))))
2.79
(define (equ? x y) (apply-generic 'equ? x y))
(put 'equ? '(scheme-number scheme-number)
(lambda (x y) (= x y)))
(put 'equ? '(rational rational)
(lambda (x y)
(and (= (numer x) (numer y))
(= (denom x) (denom y)))))
(put 'equ? '(complex complex)
(lambda (x y)
(and (= (real-part x) (real-part y))
(= (imag-part x) (imag-part y)))))
(put 'equ? '(complex complex)
(lambda (x y)
(and (= (magnitude x) (magnitude x))
(= (angle x) (angle y)))))
这里要注意调用复数时不要忘了2.77的内容
2.80
(define (=zero? x) (apply-generic '=zero? x))
(put '=zero? '(scheme-number)
(lambda (x) (= x 0)))
(put '=zero? '(rational)
(lambda (x) (= (number x) 0)))
(put '=zero? '(complex)
(lambda (x) (and (= 0 (real-part x)) (= 0 (imag-part x)))))
(put '=zero? '(complex)
(lambda (x) (= 0 (magnitude x))))
2.81
(a)调用exp过程时,解释器会进入假死状态
(b)实际上解释器进入了一个无限循环,一直在查找那个不存在的通用操作
(c)
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(if (eq? type1 type2)
(error "No method for these types" (list op type-tags))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags)))))))
(error "No method for these types"
(list op type-tags)))))))
2.82
先查找到里面的最高层级,然后将里面的数据类型全部升级成最高层级但是这种涉及到了排序和赋值,且是2.83的raise想法,显然超出了范围,题目的意思是进行双循环来进行这个过程
(define (apply-generic op . args)
(define (no-method type-tags)
(error "No method for these types"
(list op type-tags)))
(define (type-tags args)
(map type-tag args))
; 对每一个参数尝试进行强制类型转换
(define (try-coerce-to target)
(map (lambda (origin)
(if (eq? (type-tag origin) (type-tag target))
(lambda (x) x) ; 如果类型一致,不进行转换
(let ((coercor (get-coercion (type-tag origin) (type-tag target))))
(if coercor
(coercor origin)
origin))))
args))
(define (iterate next)
(if (null? next)
(no-method (type-tags args))
(let ((coerced (try-coerce-to (car next))))
(let ((proc (get op (type-tags coerced))))
(if proc
(apply proc (map contents coerced))
(iterate (cdr next)))))))
(let ((proc (get op (type-tags args))))
(if proc
(apply proc (map contents args))
(iterate args))))
来源于https://blog.csdn.net/ilongchaos/article/details/143871877
2.83
(define (raise x) (apply-generic 'raise x))
(put 'raise '(scheme-number) (lambda (x) (make-rational x 1)))
(put 'raise '(rational) (lambda (x) (make-complex-from-real-imag x 0)))
2.84
(define (raise-into x y)
(let ((raised-x (raise x)))
(cond ((equal? (type-tag x) (type-tag y)) x)
((equal? (type-tag x) (type-tag raised-x)) #f)
(else (raise-into (raise x) y)))))
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((a1 (car args))
(a2 (cadr args))
(raised-a1 (raise-into a1 a2))
(raised-a2 (raise-into a2 a1)))
(cond (raised-a1 (apply-generic op raised-a1 a2))
(raised-a2 (apply-generic op a1 raised-a2))
(else (error "No method for these types"
(list
op
type-tags)))))
(error
"No method for these types -- APPLY-GENERIC"
(list op type-tags)))))))
2.85
(define (project x)
(apply-generic 'project x))
(put 'project '(scheme-number)
(lambda (x) (make-scheme-number x)))
(put 'r-eq? '(scheme-number scheme-number)
(lambda (x y) (eq? x y)))
(put 'project '(rational)
(lambda (x)
(make-scheme-number
(car (integer-divide (numer x) (denom x))))))
(put 'r-eq? '(rational rational)
(lambda (x y) (equ-rat? x y)))
(put 'project '(real)
(lambda (x)
(make-rational (round x) 1)))
(put 'r-eq? '(real real)
(lambda (x y) (eq? x y)))
(put 'project '(rectangular)
(lambda (x)
(make-real (real-part x))))
(put 'r-eq? '(rectangular rectangular)
(lambda (x y) (and (= (real-part x) (real-part y))
(= (imag-part x) (imag-part y)))))
(put 'project '(polar)
(lambda (x)
(make-real (real-part x))))
(put 'r-eq? '(polar polar)
(lambda (x y) (and (= (magnitude x) (magnitude y))
(= (angle x) (angle y)))))
(put 'project '(complex)
(lambda (x)
(apply-generic 'project x)))
(put 'r-eq? '(complex complex) r-eq?)
(define (drop x)
(cond ((equal? (project x) x) x)
((r-eq? (raise (project x)) x)
(drop (project)))
(else x)))
2.86
https://github.com/dstodolny/sicp/blob/master/2.86.scm
(define (sine x) (apply-generic 'sine x))
(define (cosine x) (apply-generic 'cosine x))
;; scheme-number package
(put 'sine 'scheme-number
(lambda (x) (tag (sin x))))
(put 'cosine 'scheme-number
(lambda (x) (tag (cos x))))
;; rational package
(put 'sine 'rational
(lambda (x) (tag (sin (div (numer x) (denom x))))))
(put 'cosine 'rational
(lambda (x) (tag (cos (div (numer x) (denom x))))))
;; complex package
(define (add-complex z1 z2)
(make-from-real-imag (add (real-part z1) (real-part z2))
(add (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (sub (real-part z1) (real-part z2))
(sub (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (mul (magnitude z1) (magnitude z2))
(add (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (div (magnitude z1) (magnitude z2))
(sub (angle z1) (angle z2))))
就是把sin,cos加进之前的包里,然后对复数定义的运算可以由基础的add,sub,mul,div即其他数据类型能完成的操作来组成。
2.87
(define (=zero-iter? L)
(or (empty-termlist? L)
(and (=zero? (coeff (first-term L)))
(=zero-iter? (rest-terms L)))))
(put '=zero? '(polynomial)
(lambda (x)
(=zero-iter? (term-list x))))
2.88
(put 'negative '(scheme-number)
(lambda (x) (tag (- x))))
(define (negative-poly p)
(if (empty-termlist? L)
(the-empty-termlist)
(adjoin-term
(make-term (order (first-term))
(negative (coeff (first-term))))
(negative-poly (rest-terms p)))))
(put 'negative '(polynomial)
(lambda (p)
(tag (make-poly (variable p)
(negative-poly (term-list p))))))
(define (sub x y)
(apply-generic 'add x (negative y)))
2.89
https://github.com/dstodolny/sicp/blob/master/2.89.scm
(define (install-polynomial-package)
(define (make-poly variable term-list)
(cons variable term-list))
(define (variable p) (car p))
(define (term-list p) (cdr p))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (adjoin-term term term-list)
(if (=zero? (coeff term))
term-list
((eq? (order term) (length term-list)) (cons (coeff term) term-list))
(else
(adjoin-term term (cons 0 term-list)))))
(define (the-empty-termlist) '())
(define (first-term term-list) (list (- (length term-list) 1) (car term-list)))
(define (rest-terms term-list) (cdr term-list))
(define (empty-termlist? term-list) (null? term-list))
(define (make-term order coeff) (list order coeff))
(define (order term) (car term))
(define (coeff term) (cadr term))
(define (add-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(add-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- ADD-POLY"
(list p1 p2))))
(define (add-terms L1 L2)
(cond ((empty-termlist? L1) L2)
((empty-termlist? L2) L1)
(else
(let ((t1 (first-term L1)) (t2 (first-term L2)))
(cond ((> (order t1) (order t2))
(adjoin-term
t1 (add-terms (rest-terms L1) L2)))
((< (order t1) (order t2))
(adjoin-term
t2 (add-terms L1 (rest-terms L2))))
(else
(adjoin-term
(make-term (order t1)
(add (coeff t1) (coeff t2)))
(add-terms (rest-terms L1)
(rest-terms L2)))))))))
(define (mul-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(mul-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- MUL-POLY"
(list p1 p2))))
(define (mul-terms L1 L2)
(if (empty-termlist? L1)
(the-empty-termlist)
(add-terms (mul-term-by-all-terms (first-term L1) L2)
(mul-terms (rest-terms L1) L2))))
(define (mul-term-by-all-terms t1 L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((t2 (first-term L)))
(adjoin-term
(make-term (+ (order t1) (order t2))
(mul (coeff t1) (coeff t2)))
(mul-term-by-all-terms t1 (rest-terms L))))))
(define (=zero-all-terms? L)
(or (empty-termlist? L)
(and (=zero? (coeff (first-term L)))
(=zero-all-terms? (rest-terms L)))))
(define (minus-all-terms L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((current-term (first-term L)))
(cons (make-term (order current-term)
(minus (coeff current-term)))
(minus-all-terms (rest-terms L))))))
(define (tag p) (attach-tag 'polynomial p))
(put 'add '(polynomial polynomial)
(lambda (p1 p2) (tag (add-poly p1 p2))))
(put 'mul '(polynomial polynomial)
(lambda (p1 p2) (tag (mul-poly p1 p2))))
(put 'make 'polynomial
(lambda (var terms) (tag (make-poly var terms))))
(put '=zero? '(polynomial)
(lambda (p)
(=zero-all-terms? (term-list p))))
(put 'minus '(polynomial)
(lambda (p)
(tag (make-poly (variable p)
(minus-all-terms (term-list p))))))
'done)
(define (make-polynomial var terms)
((get 'make 'polynomial) var terms))
(define (make-scheme-number n)
((get 'make 'scheme-number) n))
(define (=zero? x)
(apply-generic '=zero? x))
(define (add x y)
(apply-generic 'add x y))
(define (minus x)
(apply-generic 'minus x))
(define (sub x y)
(apply-generic 'add x (minus y)))
(define (=equ? x y)
(apply-generic '=equ? x y))
2.90
(define (install-dense-package)
(define (make-poly variable term-list)
(cons variable term-list))
(define (variable p) (car p))
(define (term-list p) (cdr p))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (adjoin-term term term-list)
(cond ((=zero? (coeff term)) term-list)
((eq? (order term) (length term-list)) (cons (coeff term) term-list))
(else
(adjoin-term term (cons 0 term-list)))))
(define (the-empty-termlist) '())
(define (first-term term-list) (list (- (length term-list) 1) (car term-list)))
;; (define (rest-terms term-list) (cdr term-list))
(define (empty-termlist? term-list) (null? term-list))
(define (make-term order coeff) (list order coeff))
(define (order term) (car term))
(define (coeff term) (cadr term))
(define (add-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(add-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- ADD-POLY"
(list p1 p2))))
(define (add-terms L1 L2)
(cond ((empty-termlist? L1) L2)
((empty-termlist? L2) L1)
(else
(let ((t1 (first-term L1)) (t2 (first-term L2)))
(cond ((> (order t1) (order t2))
(adjoin-term
t1 (add-terms (rest-terms L1) L2)))
((< (order t1) (order t2))
(adjoin-term
t2 (add-terms L1 (rest-terms L2))))
(else
(adjoin-term
(make-term (order t1)
(add (coeff t1) (coeff t2)))
(add-terms (rest-terms L1)
(rest-terms L2)))))))))
(define (mul-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(mul-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- MUL-POLY"
(list p1 p2))))
(define (mul-terms L1 L2)
(if (empty-termlist? L1)
(the-empty-termlist)
(add-terms (mul-term-by-all-terms (first-term L1) L2)
(mul-terms (rest-terms L1) L2))))
(define (mul-term-by-all-terms t1 L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((t2 (first-term L)))
(adjoin-term
(make-term (+ (order t1) (order t2))
(mul (coeff t1) (coeff t2)))
(mul-term-by-all-terms t1 (rest-terms L))))))
(define (=zero-all-terms? L)
(or (empty-termlist? L)
(and (=zero? (coeff (first-term L)))
(=zero-all-terms? (rest-terms L)))))
(define (tag p) (attach-tag 'dense p))
(put 'make-poly 'dense
(lambda (var terms) (tag (make-poly var terms))))
(put 'add '(dense dense)
(lambda (p1 p2) (tag (add-poly p1 p2))))
(put 'mul '(dense dense)
(lambda (p1 p2) (tag (mul-poly p1 p2))))
'done)
(define (install-sparse-package)
(define (make-poly variable term-list)
(cons variable term-list))
(define (variable p) (car p))
(define (term-list p) (cdr p))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (adjoin-term term term-list)
(if (=zero? (coeff term))
term-list
(cons term term-list)))
(define (the-empty-termlist) '())
(define (first-term term-list) (car term-list))
;; (define (rest-terms term-list) (cdr term-list))
(define (empty-termlist? term-list) (null? term-list))
(define (make-term order coeff) (list order coeff))
(define (order term) (car term))
(define (coeff term) (cadr term))
(define (add-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(add-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- ADD-POLY"
(list p1 p2))))
(define (add-terms L1 L2)
(cond ((empty-termlist? L1) L2)
((empty-termlist? L2) L1)
(else
(let ((t1 (first-term L1)) (t2 (first-term L2)))
(cond ((> (order t1) (order t2))
(adjoin-term
t1 (add-terms (rest-terms L1) L2)))
((< (order t1) (order t2))
(adjoin-term
t2 (add-terms L1 (rest-terms L2))))
(else
(adjoin-term
(make-term (order t1)
(add (coeff t1) (coeff t2)))
(add-terms (rest-terms L1)
(rest-terms L2)))))))))
(define (mul-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(mul-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- MUL-POLY"
(list p1 p2))))
(define (mul-terms L1 L2)
(if (empty-termlist? L1)
(the-empty-termlist)
(add-terms (mul-term-by-all-terms (first-term L1) L2)
(mul-terms (rest-terms L1) L2))))
(define (mul-term-by-all-terms t1 L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((t2 (first-term L)))
(adjoin-term
(make-term (+ (order t1) (order t2))
(mul (coeff t1) (coeff t2)))
(mul-term-by-all-terms t1 (rest-terms L))))))
(define (=zero-all-terms? L)
(or (empty-termlist? L)
(and (=zero? (coeff (first-term L)))
(=zero-all-terms? (rest-terms L)))))
(define (tag p) (attach-tag 'sparse p))
(put 'make-poly 'sparse
(lambda (var terms) (tag (make-poly var terms))))
(put 'add '(sparse sparse)
(lambda (p1 p2) (tag (add-poly p1 p2))))
(put 'mul '(sparse sparse)
(lambda (p1 p2) (tag (mul-poly p1 p2))))
'done)
(define (install-polynomial-package)
(define (make-from-dense variable term-list)
((get 'make-poly 'dense) variable term-list))
(define (make-from-sparse variable term-list)
((get 'make-poly 'sparse) variable term-list))
(define (add-poly p1 p2)
(apply-generic 'add-poly p1 p2))
(define (tag p) (attach-tag 'polynomial p))
(put 'add '(polynomial polynomial)
(lambda (p1 p2) (tag (add p1 p2))))
(put 'mul '(polynomial polynomial)
(lambda (p1 p2) (tag (mul p1 p2))))
(put 'make-from-dense 'polynomial
(lambda (var terms) (tag (make-from-dense var terms))))
(put 'make-from-sparse 'polynomial
(lambda (var terms) (tag (make-from-sparse var terms))))
'done)
(define (make-polynomial-from-dense var terms)
((get 'make-from-dense 'polynomial) var terms))
(define (make-polynomial-from-sparse var terms)
((get 'make-from-sparse 'polynomial) var terms))
(define (make-scheme-number n)
((get 'make 'scheme-number) n))
(define (add x y)
(apply-generic 'add x y))
(define (mul x y)
(apply-generic 'mul x y))
(define (=zero? x)
(apply-generic '=zero? x))
2.91
(define (div-terms L1 L2)
(if (empty-terlist? L1)
(list (the-empty-termlist) (the-empty-termlist))
(let ((t1 (first-term L1)
t2 (first-term L2)))
(if (> (order t2) (order t1))
(list (the-empty-termlist) L1)
(let ((new-c (div (coeff t1) (coeff t2)))
(new-o (- (order t1) (order t2))))
(let ((rest-of-result
(div-terms (add-terms
L1
(minus-all-terms
(mul-term-by-all-terms
(make-term new-o new-c)
L2)))
L2)))
(list (adjoin-term (make-term new-o new-c)
(car rest-of-result))
(cadr rest-of-result))))))))
(define (div-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(let ((answer (div-terms (term-list p1)
(term-list p2))))
(list (tag (make-poly (variable p1) (car answer)))
(tag (make-poly (variable p2) (cadr answer))))
(error "different var!"))))
(put 'div '(polynomial polynomial)
(lambda (p1 p2) (div-poly p1 p2)))
(define (div x y)
(apply-generic 'div x y))
2.92
https://github.com/dstodolny/sicp/blob/master/2.92.scm
(define (normalize p v)
(make-poly v (adjoin-term
(make-term 0 (tag p))
(the-empty-termlist))))
(define (mul-poly p1 p2)
(cond ((variable<? (variable p1) (variable p2))
(mul-poly p1 (normalize p2 (variable p1))))
((variable>? (variable p1) (variable p2))
(mul-poly p2 p1))
(else (make-poly (variable p1)
(mul-terms (term-list p1)
(term-list p2))))))
(define (add-poly p1 p2)
(cond ((same-variable? (variable p1) 'fallback-var)
(add-poly (make-poly (variable p2) (term-list p1))
p2))
((same-variable? (variable p2) 'fallback-var)
(add-poly p1
(make-poly (variable p1) (term-list p2))))
((variable<? (variable p1) (variable p2))
(add-poly p1 (normalize p2 (variable p1))))
((variable>? (variable p1) (variable p2))
(add-poly (p2 p1)))
(else (make-poly (variable p1)
(add-terms (term-list p1)
(term-list p2))))))
(define (variable<? v1 v2)
(string<? (symbol->string v1) (symbol->string v2)))
(define (variable>? v1 v2)
(variable<? v2 v1))
2.93
(define (make-rat n d)
(list n d))
2.94
(define (remainder-terms L1 L2)
(cadr (div-terms L1 L2)))
(define (gcd-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(gcd-terms (term-list p1) (term-list p2)))
(error "different var!")))
(put 'greatest-common-divisor '(polynomial polynomial)
(lambda (p1 p2) (tag (gcd-poly p1 p2))))
(put 'greatest-common-divisor x y
(lambda (x y) (gcd x y)))
(define (greatest-common-divisor x y)
(apply-generic 'greatest-common-divisor x y))
2.95
(define (gcd-terms a b)
(if (empty-termlist? b)
a
(gcd-terms b (remainder-terms a b))))
(trace gcd-terms)
(define (show x) (display x) (newline))
(define ps1 (make-sparse-polynomial 'x '((2 1) (1 -2) (0 1))))
(define ps2 (make-sparse-polynomial 'x '((2 11) (0 7))))
(define ps3 (make-sparse-polynomial 'x '((1 13) (0 5))))
(define qs1 (mul ps1 ps2))
(define qs2 (mul ps1 ps3))
(show (greatest-common-divisor qs1 qs2))
(polynomial x sparse (2 1458/169) (1 -2916/169) (0 1458/169))
(define pd1 (make-dense-polynomial 'x '(1 -2 1)))
(define pd2 (make-dense-polynomial 'x '(11 0 7)))
(define pd3 (make-dense-polynomial 'x '(13 5)))
(define qd1 (mul pd1 pd2))
(define qd2 (mul pd1 pd3))
(show (greatest-common-divisor qd1 qd2))
>(gcd-terms {11 -22 18 -14 7} {13 -21 3 5})
>(gcd-terms {13 -21 3 5} {1458/169 -2916/169 1458/169})
>(gcd-terms {1458/169 -2916/169 1458/169} ())
<{1458/169 -2916/169 1458/169}
(polynomial x dense 1458/169 -2916/169 1458/169)
2.96
https://github.com/dstodolny/sicp/blob/master/2.96.scm
(define (pseudoremainder-terms L1 L2)
(let ((factor (expt (coeff (first-term L2)) (+ 1 (order (first-term L1)) (- (order (first-term L2)))))))
(cadr (div-terms (mul-term-by-all-terms (make-term 0 factor) L1) L2))))
(define (gcd-terms a b)
(if (empty-termlist? b)
(let* ((coeff-list (map coeff a))
(gcd-coeff (apply gcd coeff-list)))
(div-terms a (adjoin-term (make-term 0 gcd-coeff) (the-empty-termlist))))
(gcd-terms b (pseudoremainder-terms a b))))
2.97
(put 'reduce '(scheme-number scheme-number)
(lambda (x y) (map tag (reduce-integers x y))))
(define (reduce-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(let ((result (reduce-terms (term-list p1) (term-list p2))))
(list (tag (make-poly (variable p1) (car result)))
(tag (make-poly (variable p1) (cadr result)))))
(error "Polys not in same var -- REDUCE-POLY"
(list p1 p2))))
(define (reduce-terms n d)
(let ((gcd-nd (gcd-terms n d)))
(list (car (div-terms n gcd-nd))
(car (div-terms d gcd-nd)))))
(put 'reduce '(polynomial polynomial) reduce-poly)
(define (reduce x y)
(apply-generic 'reduce x y))