课本提供的一些代码
(define (sqrt x)
(sqrt-iter 1.0 x))
(define (improve guess x)
(average guess (/ x guess)))
(define (average x y)
(/ (+ x y) 2))
(define (expt b n)
(if (= n 0)
1
(* b (expt b (- n 1)))))
(define (expt-iter b counter product)
(if (= counter 0)
product
(expt-iter b
(- counter 1)
(* b product))))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1))))))
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
(= (remainder b a) 0))
(define (prime? n)
(= n (smallest-divisor n)))
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(remainder (square (expmod base (/ exp 2) m))
m))
(else
(remainder (* base (expmod base (- exp 1) m))
m))))
(define (fermat-test n)
(define (try-it a)
(= (expmod a n n) a))
(try-it (+ 1 (random (- n 1)))))
(define (fast-prime? n times)
(cond ((= times 0) true)
((fermat-test n) (fast-prime? n (- times 1)))
(else false)))
(define (timed-prime-test n)
(newline)
(display n)
(start-prime-test n (runtime)))
(define (start-prime-test n start-time)
(if (prime? n)
(report-prime (- (runtime) start-time))))
(define(report-prime elapsed-time)
(display "***")
(display elapsed-time))
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
1.1
手打一遍,运行就可以了
10
12
8
3
6
19
#f
4
16
6
16
1.2
还是脑袋过一遍,再手打
(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5)))))
(* 3 (- 6 2) (- 2 7)))
1.3
简单用cond来进行选择
(define (max-tri-sum a b c)
(cond ((and (< a b) (< a c)) (+ b c))
((and (< b a) (< b c)) (+ a c))
((and (< c b) (< c a)) (+ a b))))
1.4
(define (a-plus-abs-b a b)
((if (> b 0) + -) a b))
如果b>0进行a+b的运算
反之进行a-b运算,这样做其实是把函数也当作参数传递了
1.5
(define (p) (p))
(define (test x y)
(if (= x 0)
0
y))
(test 0 (p))
应用序是传入的参数立刻进行求值,而正则序是有需要时才求值,所以应用序在调用该函数时会陷入无限循环里,而正则序不会。
1.6
计算会报错,主要是因为递归深度太深导致的栈溢出,尽管scheme自带尾递归优化,但是这里的new-if并不是尾递归(sqrt-iter的值需要传入new-if里)
1.7
在极小极大时候,都输出不正确,极小有数值偏差,极大又陷入计算循环中
这里看了习题解,定义了新的guess和sqrt
(define (good-enough? old-guess new-guess)
(> 0.01
(/ (abs (- new-guess old-guess))
old-guess)))
(define (sqrt-iter guess x)
(if (good-enough? guess (improve guess x))
(improve guess x)
(sqrt-iter (improve guess x)
x)))
1.8
注意的是给出的公式是比求平均数更精确的方法,因此改进improve就行,这题没有要求在大数量和小数量较准确,所以就可以沿用先前的good-enough?了。
(define (abs x)
(cond ((< x 0) (- x))
((= x 0) x)
((> x 0) x)))
(define (improve guess x)
(/ (+ (/ x (* guess guess)) (* 2 guess))
3))
(define (good-enough? guess x)
(< (abs (- (* guess guess guess) x))
0.01))
(define (curt-iter guess x)
(if (good-enough? guess x)
guess
(curt-iter (improve guess x)
x)))
(define (curt x)
(curt-iter 1.0 x))
1.9
见习题集的回答
递归
(define (plus a b)
(if (= a 0)
b
(inc (plus (dec a) b))))
(plus 3 5)
(inc (plus 2 5))
(inc (inc (plus 1 5)))
(inc (inc (inc (plus 0 5))))
(inc (inc (inc 5)))
(inc (inc 6))
(inc 7)
8
迭代
(define (plus a b)
(if (= a 0)
b
(plus (dec a) (inc b))))
(plus 3 5)
(plus 2 6)
(plus 1 7)
(plus 0 8)
8
1.10
(define (A x y)
(cond ((= y 0)
0)
((= x 0)
(* 2 y))
((= y 1)
2)
(else
(A (- x 1)
(A x (- y 1))))))
(A 1 10) -> 1024
(A 2 4) -> 65536
(A 3 3) -> 65536
RTFSC我们可以知道,(f n)是2n,(g n)是2^n,由前面我们可以得到(h n)是2的2次幂的2次幂以此循环…..
1.11
递归
(define (c-finb n)
(cond ((< n 3) n)
(else (+ (c-finb (- n 1)) (* 2 (c-finb (- n 2))) (* 3 (c-finb (- n 3)))))))
迭代
(define( d-finb-iter first second third n)
(if (= n 3)
(+ (* 3 first) (* 2 second) third)
(d-finb-iter
second
third
(+ (* 3 first) (* 2 second) third)
(- n 1)) ))
(define (d-finb n)
(if (< n 3)
n
(d-finb-iter 0 1 2 n)))
1.12
不知道题目什么意思,看了习题解发现是翻译错误。。。
以下是习题解答案
(define (pascal row col)
(cond ((> col row)
(error "unvalid col value"))
((or (= col 0) (= row col))
1)
(else (+ (pascal (- row 1) (- col 1))
(pascal (- row 1) col)))))
1.13
证明就不细致自己写了想不出,以下复刻习题解的回答

1.14
这种图都没什么好说的(直接抄把)
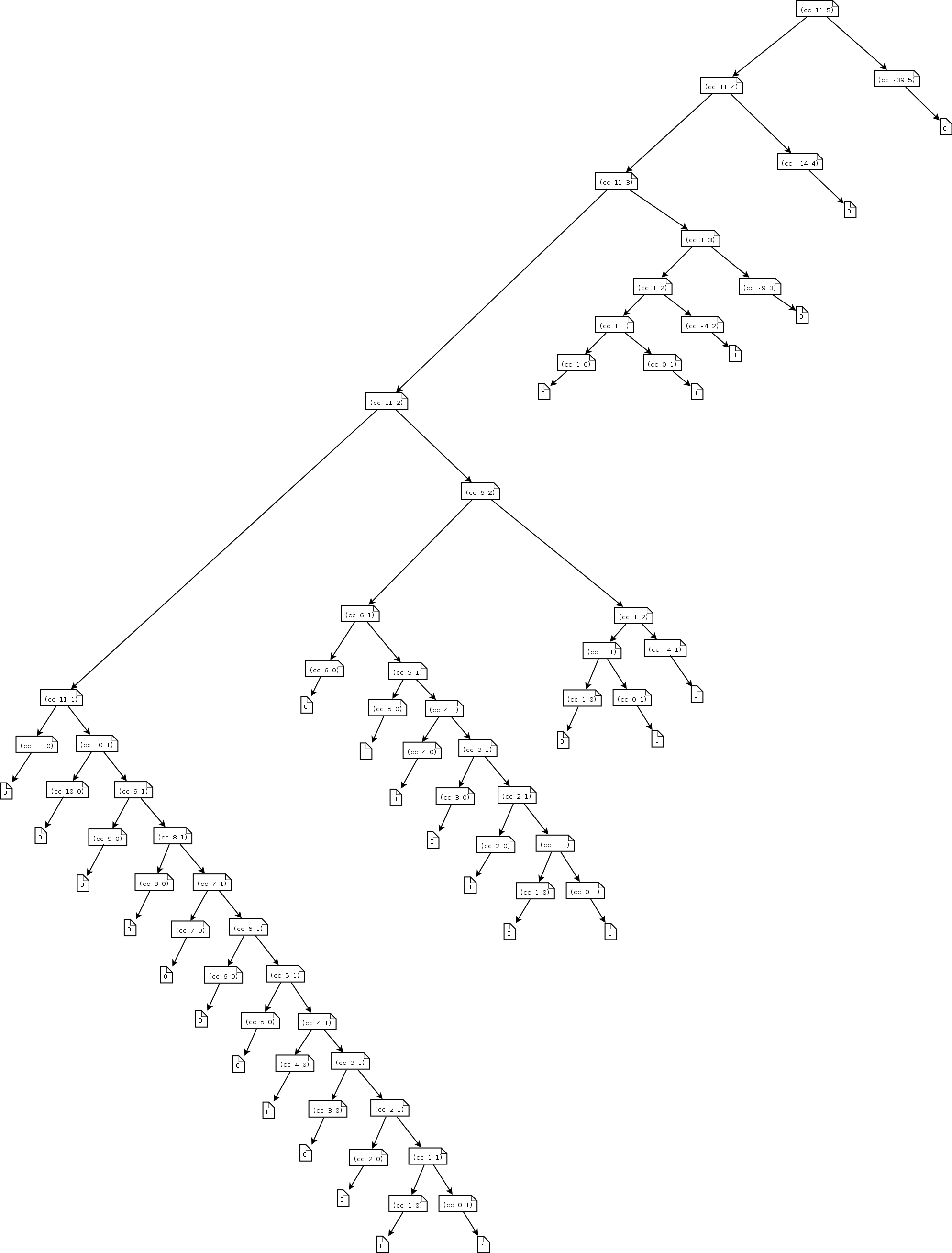
1.15
a:演算可以得到为5次
b:程序为递归程序,所以时间和空间复杂度都是O(loga)
1.16
(define (square x)
(* x x))
(define (even? n)
(= (remainder n 2) 0))
(define (fast-expt-d b n)
(fast-expt-iter b n 1))
(define (fast-expt-iter b n product )
(cond ((= n 0) product)
((even? n) (fast-expt-iter (square b) (/ n 2) product ))
(else (fast-expt-iter b (- n 1) (* b product) ))))
主要卡在了偶数时只更新b的值,我刚开始一并更新了product的值导致过大
1.17
实际上只是仿写一下幂乘就行了,even?在上题里有,而且它也是自带的,可以直接调用。
(define (double x)
(* 2 x))
(define (halve x)
(/ x 2))
(define (mul a b)
(cond((= b 0) 0)
((even? b) (mul (double a) (halve b)))
(else (+ a (mul a (- b 1))))
))
1.18
这就是1.17的迭代形式
(define (double x)
(* 2 x))
(define (halve x)
(/ x 2))
(define (fast-mul a b)
(fast-mul-iter a b 0)
)
(define (fast-mul-iter a b product)
(cond ((= b 0) product)
((even? b) (fast-mul-iter (double a) (halve b) product))
(else (fast-mul-iter a (- b 1) (+ product a)))))
1.19
证明:
a \rightarrow bq + aq + ap
\rightarrow (bp + aq)q + (bq + aq + ap)q + (bq + aq + ap)p
= b(2pq + q^2) + a(2pq + q^2) + a(q^2 + p^2)
b \rightarrow bp+aq
\rightarrow (bp+aq)p+(bq+aq+ap)q
=b(q^2+p^2)+a(2pq+q^2)
所以我们可以得出
p’=(q^2+p^2)
q’=(2pq+q^2)
通过这个我们可以试着去实现我们的代码:
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q n)
(cond ((= n 0)
b)
((even? n)
(fib-iter a
b
(+ (square p) (square q))
(+ (* 2 p q) (square q))
(/ n 2)))
(else
(fib-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- n 1)))))
其实就是把我们计算的结果应用在函数上就行了
1.20
自己过一遍模拟过程就行了,这里就参考解题集了写的比我好
应用序:
(gcd 206 40)
(gcd 40 6) ; (gcd 40 (remainder 206 40)
(gcd 6 4) ; (gcd 6 (remainder 40 6))
(gcd 4 2) ; (gcd 4 (remainder 6 4))
(gcd 2 0) ; (gcd 2 (remainder 2 2))
2
一共调用了5步
而正则序呢在迭代的过程需要计算条件即if中的判断,模拟完可知计算条件一共调用了14次,再加上过程调用的4次,共18次。
1.21
(smallest-divisor 199)
199
(smallest-divisor 1999)
1999
(smallest-divisor 19999)
7
1.22
专门设一个参数来记录开始时间,另一个参数来记录已经找到的素数个数,完成查找三个时输出完整运行时间(差值)。采用奇数生成器来节省时间,测试素数的函数可以复用上面的内容,
(define (next-odd n)
(if(odd? n)
(+ 2 n)
(+ 1 n)))
(define (third-prime n w starttime)
(cond ((= w 0)
(display (- (runtime) starttime))
)
((prime? n)
(third-prime n (- w 1) starttime)
)
(else (third-prime (next-odd n) w starttime))))
(define (search-for-prime n)
(third-prime n 3 (runtime)))
(search-for-prime 1000)
7
(search-for-prime 10000)
12
(search-for-prime 100000)
25
(search-for-prime 1000000)
104(70-150)
这里测试发现误差还挺大的(
但是倍数不是\sqrt{10}所以在机器上运行的时间不正比于计算的步数。
1.23
(define (next x)
(if (= x 2)
3
(+ x 2)
))
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (next test-divisor)))))
对timed-prime-test进行修改
(define (start-prime-test n start-time)
(smallest-divisor n)
(report-prime (- (runtime) start-time)))
修改前:(timed-prime-test 10000) 3
修改后:(timed-prime-test 10000) 3
发现误差不大,原来是runtime的记录精度不够,习题解用的是real-time-clock,修改后测试发现运行更快了,但也不是一倍。
1.24
直接修改prime?为fast-prime?就好了
(define (start-prime-test n start-time)
(if(fast-prime? n 10)
(report-prime (- (runtime) start-time))))
测试可知速度与之前相比确实提升了,但是也不是严格按常数级别增长。一部分也有误差的原因。
1009->4 1000003->33(22-35大概…)
最多慢了八倍,最快慢了五倍,我们也可以得出来,时间复杂度在现实还要考虑到计算机运行速度,占用资源等等一系列误差。
1.25
理论上可行,但是我们快速检查时有时也需要处理非常大的数值,它的乘幂就很大,容易超出空间。而每次取余就控制了数的大小使得其便于计算,而且提高了速度。
1.26
这个原因在于
(* (expmod base (/ exp 2) m)
(expmod base (/ exp 2) m))
计算了两次(expmod base (/ exp 2) m),(相当于是独立的进程被进行了两次),而(square (expmod base (/ exp 2) m))相当于自乘的是一个数值,而不是一个仍需要计算的进程,因此时间变慢了,这其实有点像编译器的常量传播。
1.27
(define (carmichael-test n)
(test 1 n))
(define (test t-number n)
(cond((= t-number n)
true)
((expmod? t-number n)
(test (+ t-number 1) n))
(else false)))
(define (expmod? t-number n)
(= (expmod t-number n n) t-number))
用脚注47的数据测试得输出结果都为#t
1.28
(define (expmod base exp m)
(cond ((= exp 0) 1)
((sqrt? base m) 0)
((even? exp)
(remainder (square (expmod base (/ exp 2) m))
m) )
(else
(remainder (* base (expmod base (- exp 1) m))
m)
)))
(define (r-test n)
(define (try-it a)
(= (expmod a (- n 1) n) 1))
(try-it (+ 1 (random (/ (- n 1) 2)))))
(define (sqrt? a n)
(and(not (= a 1))
(not (= a (- n 1)))
(= 1 (remainder (square a) n))))
主要还是照着题目的要求来写代码,在expmod里新增了一个模块sqrt?用来检测非平凡根。测试时候发现有时候会#t时会#f,还以为自己写错了,查资料才发现原来是这个检查也是概率函数,至少测试n/2次后结果才稳定下来。
1.29
把一些函数封装在simpson里面,调用书本上的sum。
(define (cube x)
(* x x x))
(define (sum term a next b)
(if (> a b)
0
(+ (term a) (sum term (next a) next b))))
(define (simpson f a b n)
(define h
(/ (- b a) n))
(define (fact k)
(cond ((or (= k 0) (= k n)) 1)
((odd? k) 4)
((even? k) 2)))
(define (y k)
(f (+ a (* k h))))
(define (term k)
(/ (* h (y k) (fact k)) 3)
)
(define (next k)
(+ k 1))
(sum term 0 next n)
)
我的DrRaket输出时不是小数而是分数,没法判断精确程度,但是按理来说是更精确的。
1.30
把改变的量改为用参数形式传入就能把递归修改为迭代了。
(define(sum term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (+ (term a) result))))
(iter a 0))
1.31
这里将递归和迭代形式和对应的实现pi函数分隔开来
递归
(define (product-recursion start term next end)
(if (> start end)
1
(* (term start) (product-recursion (next start) term next end))))
(define (pi-recursion n)
(define (next x)
(+ x 1))
(define (ration k)
(if (odd? k)
(/ (+ k 1) (+ k 2))
(/ (+ k 2) (+ k 1))))
(* 4 (product-recursion 1 ration next n)))
迭代
(define (product-iter start term next end)
(define (iter start result)
(if (> start end)
result
(iter (next start) (* result (term start)))))
(iter start 1))
(define (pi-iter n)
(define (ration k)
(if (odd? k)
(/ (+ k 1) (+ k 2))
(/ (+ k 2) (+ k 1))))
(define (next x)
(+ x 1))
(* 4 (product-iter 1 ration next n)))
1.32
递归
(define (accumblate combiner null-value term a next b)
(if (> a b)
null-value
(combiner
(term a)
(accumblate combiner null-value term (next a) next b))))
迭代
(define (accumblate combiner null-value term a next b)
(if(> a b)
null-value
(accumblate combiner (combiner (term a) null-value) term (next a) next b)))
(define (sum-accumblates term a b n)
(accumblate + 0 term a next b))
(define (product-accumblates term a b n)
(accumblate * 1 term a next b))
1.33
递归
(define (filtered-accumblate filter combiner null-value term a next b)
(cond ((> a b) null-value)
((filter a)(combiner
(term a)
(filtered-accumblate filter combiner null-value term (next a) next b)))
(else (combiner
null-value
(filtered-accumblate filter combiner null-value term (next a) next b)))))
迭代
(define (filtered-accumblate filter combiner null-value term a next b)
(cond((> a b) null-value)
((filter) (filtered-accumblate filter combiner (combiner (term a) null-value) term (next a) next b))
(else (accumblate combiner null-value term (next a) next b))))
题2需要两个参数所以用之前的模板不好表达,我们最好引入下文提到的lambda表达式来解决
(define (sum-prime a b)
(define (term x) x)
(define (next x) (+ x 1))
(filtered-accumblate prime? + 0 term a next b))
(define (co-prime? a b)
(and (< a b) (= (gcd a b) 1)))
(define (mul-co-prime n)
(define (term x) x)
(define (next x) (+ x 1))
(filtered-accumblate (lambda (x) (coprime? x n)) * 1 term 1 next n))
1.34
(define (f g)
(g 2))
(f f)
=>(f 2)
=>(2 2)
1.35
我们设有这么一个正方形,宽为1,长为\Phi
在里面截取一个边长为1的正方形,新矩形的长为 1,宽为 \Phi -1,且\frac{\Phi}{1}=\frac{1}{\Phi -1}即\Phi ^2=\Phi +1
也即x^2=x+1,x=1+\frac{1}{x}
即黄金分割率为此的映射
(fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0)
1.36
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(begin
(display next)
(newline)
(try next)))))
(try first-guess))
(fixed-point (lambda (x) (/ (log 1000) (log x))) 2.0) ;steps=34
(fixed-point (lambda (x) (average x (/ (log 1000) (log x)))) 2.0) ;steps=9
1.37
递归形式,k=11时能达到精确程度0.618。
(define (cont-frac n d k)
(define (next x)
(+ x 1))
(define (recursion n d k j)
(if (= j k)
(/ (n j) (d j))
(/ (n j) (+ (d j) (recursion n d k (next j))))))
(recursion n d k 1))
(cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 11)
迭代,我们可以反向操作
“`scheme
(define (cont-frac n d k)
(define (next x)
(+ x 1))
(define (iter n d k j sum)
(if (= j k)
(/ (n (- k j)) (+ (d (- k j)) sum))
(iter n d k (next j) (/ (n (- k j)) (+ (d (- k j)) sum)))))
(iter n d (- k 1) 0 0))
“`
1.38
(define (e-text k)
(define (d-number x)
(if (= (remainder (+ x 1) 3) 0)
(* 2 (/ (+ x 1) 3))
1))
(+ 2 (cont-frac (lambda (i) 1.0) d-number k)))
1.39
递归
(define (tan-cf x k)
(define (next x)
(+ x 1))
(define (recursion x d k j)
(cond ((= j 1)
(/ x (- (d j) (recursion x d k (next j)))))
((= j k)
(/ (* x x) (d j)))
(else
(/ (* x x) (- (d j) (recursion x d k (next j)))))))
(recursion x (lambda (i) (- (* 2 i) 1)) k 1))
迭代
(define (tan-cf x k)
(define (next x)
(- x 1))
(define (iter x d k sum)
(cond ((= k 1)
(/ x (- (d k) sum)))
(else
(iter x d (next k) (/ (* x x) (- (d k) sum))))))
(iter x (lambda (i) (- (* 2 i) 1)) k 0))
1.40
(define (cubic a b c)
(lambda (x) (+ (* x x x) (* a x x) (* b x) c)))
1.41
事实上就是要注意lambda向外捕获参数的过程
(define (double f)
(lambda (x) (f (f x))))
(((double (double double)) inc) 5)=>21
1.42
(define (compose f g)
(lambda (x) (f (g x))))
1.43
(define (repeated f n)
(if (= n 0)
(lambda (x) x)
(lambda (x) ((repeated f (- n 1)) (f x)))
))
1.44
(define (smooth f)
(define dx 0.00001)
(lambda (x) (/ (+ (f x) (f (- x dx)) (f (+ x dx))) 3)))
((repeated (smooth f) n) x)
1.45
\log _2n的由来和算法参考了习题解
(define (square x)
(* x x))
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(define (repeated f n)
(if (= n 0)
(lambda (x) x)
(lambda (x) ((repeated f (- n 1)) (f x)))
))
(define (average a b)
(/ (+ a b) 2))
(define (average-damp f)
(lambda (x) (average x (f x))))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1))))))
(define (n-root n)
(define (lg w)
(cond ((> (/ w 2) 1)
(+ 1 (lg (/ w 2))))
((< (/ w 2) 1)
0)
(else
1)))
(lambda (x)
(fixed-point
(repeated (average-damp
(lambda (y)
(/ x (fast-expt y (- n 1))))
) (lg n))
1.0))) ;返回的是一个过程
1.46
这里主要在思考初始的猜测值怎么引入,但没有写好,习题解对fixed-point的改变形式让我耳目一新,而且也提醒了我在lambda里面可以继续定义函数,这里就展示习题解的答法:
(define (iterative-improve close-enough? improve)
(lambda (first-guess)
(define (try guess) ;有效解决了猜测量引入和迭代的问题
(let ((next (improve guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess)))
(define (sqrt x)
(define dx 0.00001)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) dx))
(define (improve guess)
(average guess (/ x guess)))
(define (average x y)
(/ (+ x y) 2))
((iterative-improve close-enough? improve) 1.0))
define (fixed-point f first-guess)
(define tolerance 0.00001)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (improve guess)
(f guess))
((iterative-improve close-enough? improve) first-guess))